Implémentation et parcours de graphe en OcamL

Dans ce cours, nous allons uniquement utiliser la notion de graphe orienté. Un graphe est de manière peu formelle un ensemble de sommet relié par des arêtes. Une représentation d'un tel objet ressemble à l'image suivante :

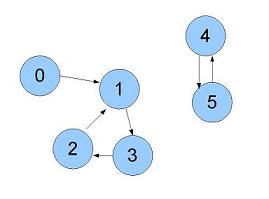
On supposera de plus que le graphe est simple (bien que l'algorithme ne change pas, on verra après pourquoi) : c'est à dire qu'il n'est pas possible qu'il y ait deux arêtes qui aillent du même sommet à un autre.

Les sommets auxquels on peut directement accéder à partir d'un sommet en n'empruntant qu'une seule arête s'appellent les voisins. Par exemple le voisin de 0 est 1, le voisin de 1 est 3. Il peut y avoir plusieurs voisins si plusieurs arêtes partent d'un sommet.

Un graphe orienté simple peut être défini comme suit :
Un graphe G est un couple (V,E) où V (vertices) est l'ensemble des sommets (nombre fini) et E (edges) l'ensemble des arêtes (ce sont des couples de sommets de V).
Par exemple, dans notre exemple, V = {0,1,2,3,4,5} et E = {(0,1), (1,3), (3,2) , (2,1),(4,5), (5,4)}.
On pourrait représenter le graphe en camL directement sous cette forme, mais cela n'est pas efficace pour les parcours (profondeur et largeur) de graphe. C'est ce que nous allons voir.

Un parcours est une procédure qui permet d'aller chercher l'ensemble des sommets accessibles à partir d'un sommet choisi et d'effectuer une opération dessus. Par exemple, dans la première figure, l'ensemble des sommets accessibles à partir de 0 sont : 1, 2 et 3. Mais l'ensemble des sommets accessibles à partir de 3 sont uniquement : 3, 2 et 1. En effet, on ne peut pas retourner au sommet 0 car il n'existe pas d'arête allant vers 0.

En pratique, on travaille récursivement sur les voisins du sommet. Dans le parcours en largeur, on parcourt les successeurs du sommet de départ par rapport à sa profondeur. On regarde tout d'abord, les successeurs séparés par une arête. Ensuite les successeurs séparés par deux arêtes et ainsi de suite. Dans le parcours en profondeur, on parcourt récursivement les voisins du sommet en allant "en profondeur". Ces deux algorithmes sont en fait très similaires et ne dépendent que de l'ordre dans lequel on choisit le futur sommet à visiter.

Afin de mieux comprendre la notion de parcours, nous allons voir un exemple sur la figure suivante.

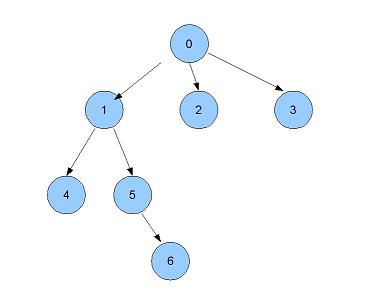
III-B-1. Exemple du parcours en largeur▲

En partant du sommet 0, le parcours en largeur donne successivement.

• On visite le sommet 0

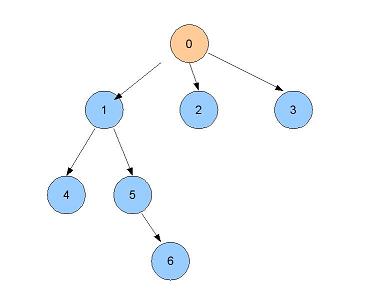
• Les voisins de distance 1 : 1, 2, 3

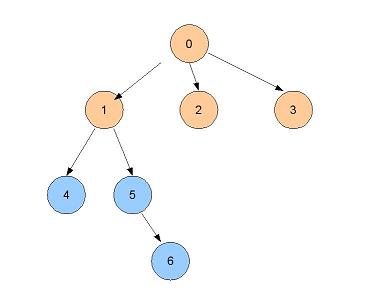
• Les voisins de distance 2 : 4, 5

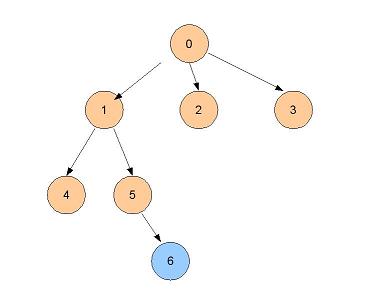
• Puis les voisins de distance 3 : 6

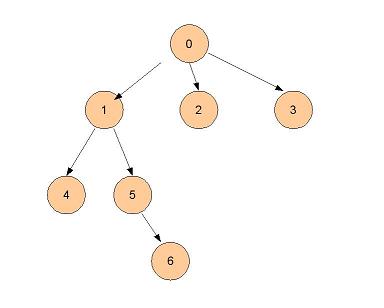
• On a parcouru tout le graphe, l'algorithme s'arrête

On va récapituler le procédure en mettant dans une liste les éléments restant à visiter.

• On visite 0, on place dans la liste les éléments restant à visiter dans l'ordre : 1, 2, 3
• On visite le premier élément de la liste 1, ses voisins sont 4 et 5, il reste à visiter 2, 3, 4, 5 (il faut bien que l'on met les éléments à la fin de la liste)
• On visite 2 qui n'a pas de voisins, il reste à visiter 3, 4, 5
• On visite 3 qui n'a pas de voisins, il reste à visiter 4, 5
• On visite 4 qui n'a pas de voisin, il reste à visiter 5
• 5 a un unique voisin, il reste donc à visiter 6
• Puis on visite le dernier sommet

Lorsque l'on ajoute les voisins à la liste des éléments à ajouter, on les place à la fin, et on lit le premier élément de la liste, cela correspond à une structure de file.

III-B-2. Exemple du parcours en profondeur▲

Le parcours en profondeur peut donner (mais ce n'est pas unique) :

• On visite le sommet 0

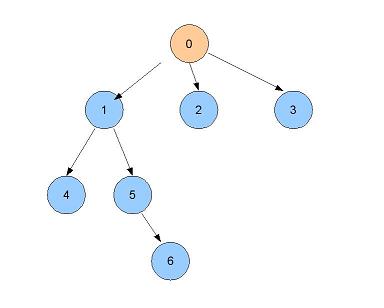
• Voisins : 1, 2, 3, on visite 1 (reste à visiter 2,3)

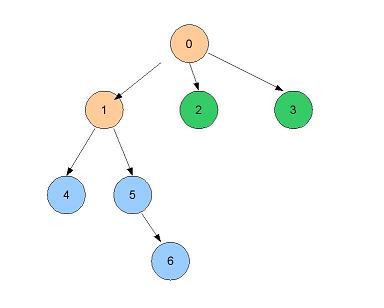
• Voisins de 1 : 4 et 5, on visite 4 (reste à visiter 5, 2, 3)

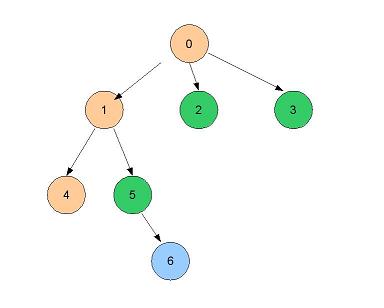
• 4 n'a plus de voisin, on visite 5 (reste à visiter 2,3)

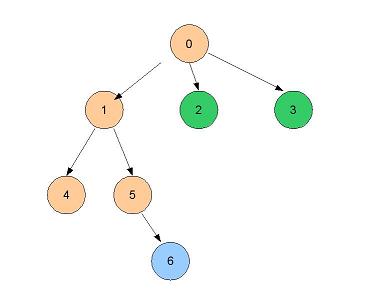
• Voisins de 5 : 6, on visite cet unique sommet (reste à visiter 2,3)

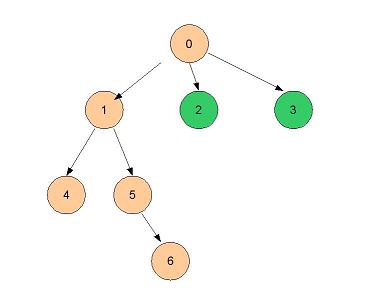
• 6 n'a pas de voisin, on retourne à 2 (reste à visiter 3)

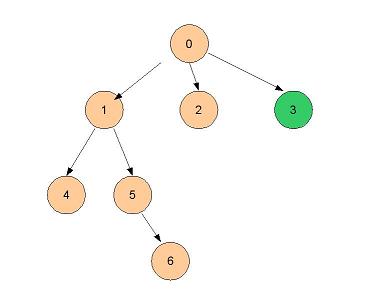
• 2 n'a pas de voisin, on retourne à 3 (il ne reste rien à visiter)

On va récapituler le procédure en mettant dans une liste les éléments restant à visiter.

• On visite 0, on place dans la liste les éléments restant à visiter dans l'ordre : 1, 2, 3
• On visite le premier élément de la liste 1, ses voisins sont 4 et 5, il reste à visiter 4, 5, 2, 3 (il faut bien que l'on met les éléments au début de la liste)
• On visite 4 qui n'a pas de voisins, il reste à visiter 5, 2, 3
• On visite 5 qui a un voisin, il reste à visiter 6, 2, 3
• On visite 6 qui n'a pas de voisin, il reste à visiter 2 et 3
• 2 n'a pas de voisin, il reste donc à visiter 3
• 3 n'a pas de voisin, le parcours est terminé

Lorsque l'on ajoute les voisins à la liste des éléments à ajouter, on les place au début, et on lit le premier élément de la liste, cela correspond à une structure de pile.

Lorsque l'on détermine les voisins d'un sommet. On sait que l'on doit tous les visiter. Une idée serait donc de mettre dans un ensemble les sommets qu'il reste à visiter. Nous n'allons pas expliciter l'implémentation d'un tel ensemble (qui correspondra à une file ou à une pile, mais nous généralisons le procédé dans un premier temps), on supposera qu'il dispose des opérations suivantes :

• [] : représente l'ensemble vide
• ensembleChoisir (Ensemble) -> element : retourne un élément de l'ensemble
• ensembleRetirer (Ensemble) -> Ensemble : retire l'élément que l'on obtient avec ensembleChoisir
• ensembleUnion(Ensemble 1, Ensemble 2) -> Ensemble : détermine la réunion des deux ensembles (on peut supposer qu'il existe des doublons)
• element appartient Ensemble -> Booléen est vrai si l'élément appartient à l'ensemble et faux sinon

À un moment du parcours, on suppose que l'on dispose des 2 ensembles suivants :

• avisiter : l'ensemble des sommets qu'il reste à visiter
• aetevisite : l'ensemble des sommets qui ont déjà été visité

L'algorithme peut s'écrire comme suit :

fonction Parcours g avisiter aetevisite=
  Si avisiter = [] alors /*Si il ne reste rien à visiter, on a fini*/
     fin;
  Sinon
     sommetcourant = ensembleChoisir(avisiter) /*sommet que l'on traite*/
     resteavisiter = ensembleRetirer(avisiter)
     Si sommetcourant appartient à aetevisite alors /*Si l'élément a déjà été visité*/
	   Parcours g aetevisite resteavisiter /*on visite les sommets suivants*/
     Sinon
       /* on ajoute au élément à visiter les voisins du sommet courant,
          et on ajoute le sommetcourant au élément qui ont été visité*/
	   Parcours g ensembleUnion(resteavisiter, voisin(g, sommetcourant)) ensembleUnion(aetevisite, sommetcourant)

Nous allons chercher à expliciter le type ensemble, cela nous permettra de définir l'implémentation du graphe afin d'optimiser le parcours.

Il faut noter que même si l'ensemble admet des doublons, l'algorithme est bon. Cela nous permet ainsi d'envisager un type liste pour l'ensemble avisiter. L'opération ensembleChoisir consistera juste à prendre le premier élément de la liste. et l'opération ensembleRetirer consistera à prendre la queue de la liste.

Ce qui devient intéressant, c'est le choix d'implémentation de l'opération ensembleUnion. Si l'on choisit d'ajouter les éléments à la queue de la liste, l'algorithme devient un parcours en largeur et si l'on choisit d'ajouter les éléments à la tête de la liste, cela devient un parcours en profondeur.

Ainsi, dans le cas du parcours en largeur, comme on ajoute les éléments à la queue de la liste, cela revient à utiliser comme implémentation du type Ensemble une file. Dans le parcours en profondeur, cela revient à utiliser une pile.

On implémente l'ensemble des arêtes du graphe par une liste de liste des successeurs.

Par exemple, sur le graphe 3, on a : [(0,[1,2,3]), (1,[4,5]), (2,[]), (3,[]), (4,[]), (5,[6]), (6,[]))

Pour le premier graphe, on a : [(0,[1]), (1,[3]), (2,[1]), (3,[2]), (4,[5]), (5,[4])]

Si par exemple, on souhaite déterminer les voisins du sommet 3, il suffit d'aller chercher le couple dont le premier élément est 3, puis de renvoyer la liste des voisins (le deuxième élément du couple).